５年生の 分数と小数 整数の関係 のソフト 横山験也のちょっと一休み
分数と小数／理解シート 整数を分数に直すには，どうすればいいの 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author VAIO Created Date PMそんなときのために帯分数を仮分数に直す方法を解説します。 先程述べた 「帯分数は『』が省略されている」 ということ、そして 分数の通分のページ で解説した 「分数の足し算は通分して分母を揃えるのが基本」 ということをきちんと抑えていれば自然と以下の計算が導けるかと思います。
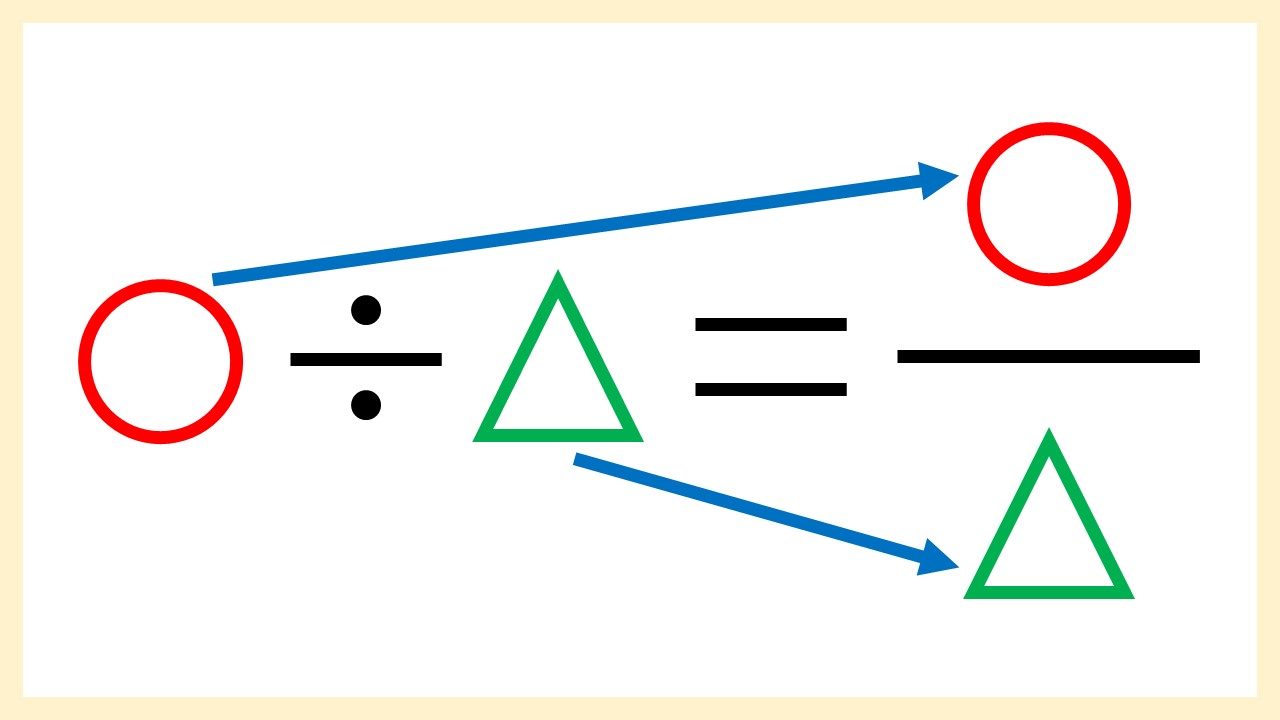
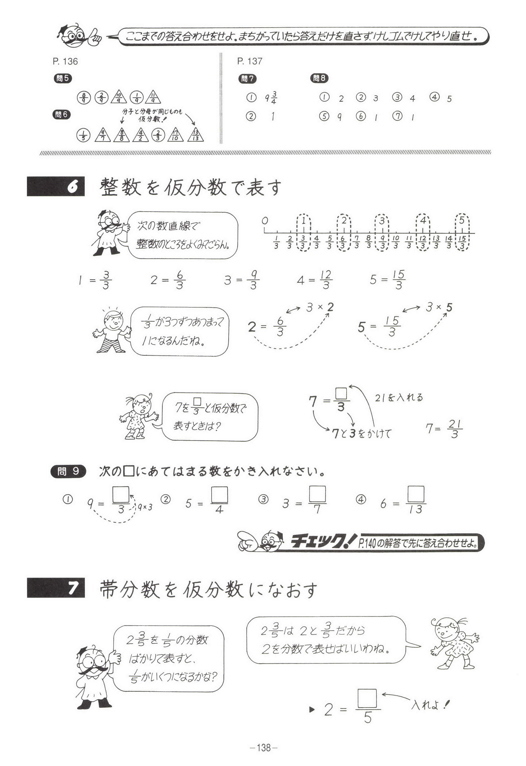
整数を分数に直す
整数を分数に直す- この記事は、分数と割り算の関係がわからない人に向けて書いています。今回は、割り算を分数に直す 1次の割り算を、分数に直しましょう。答えを整数で書いてはいけません。 （1）9÷7 （2）4÷1 （3）99÷24 （4）40÷5 （5）8÷8 解答編 1次の割り算を、分数に直しましょう。答えをこれは、「分母が基準の量」となる分数と同じです： =01 (2) 比率を百分率（パーセント）で表す： 01=10% ⇒ このように、 割合（パーセント）を求める問題 では (1) 基準の量で割って割合を比率を小数で求める： （比較する量） ÷（基準の量） 分数で書けば (2) 小数をパーセントに直す の2段階
City Saitama Jp
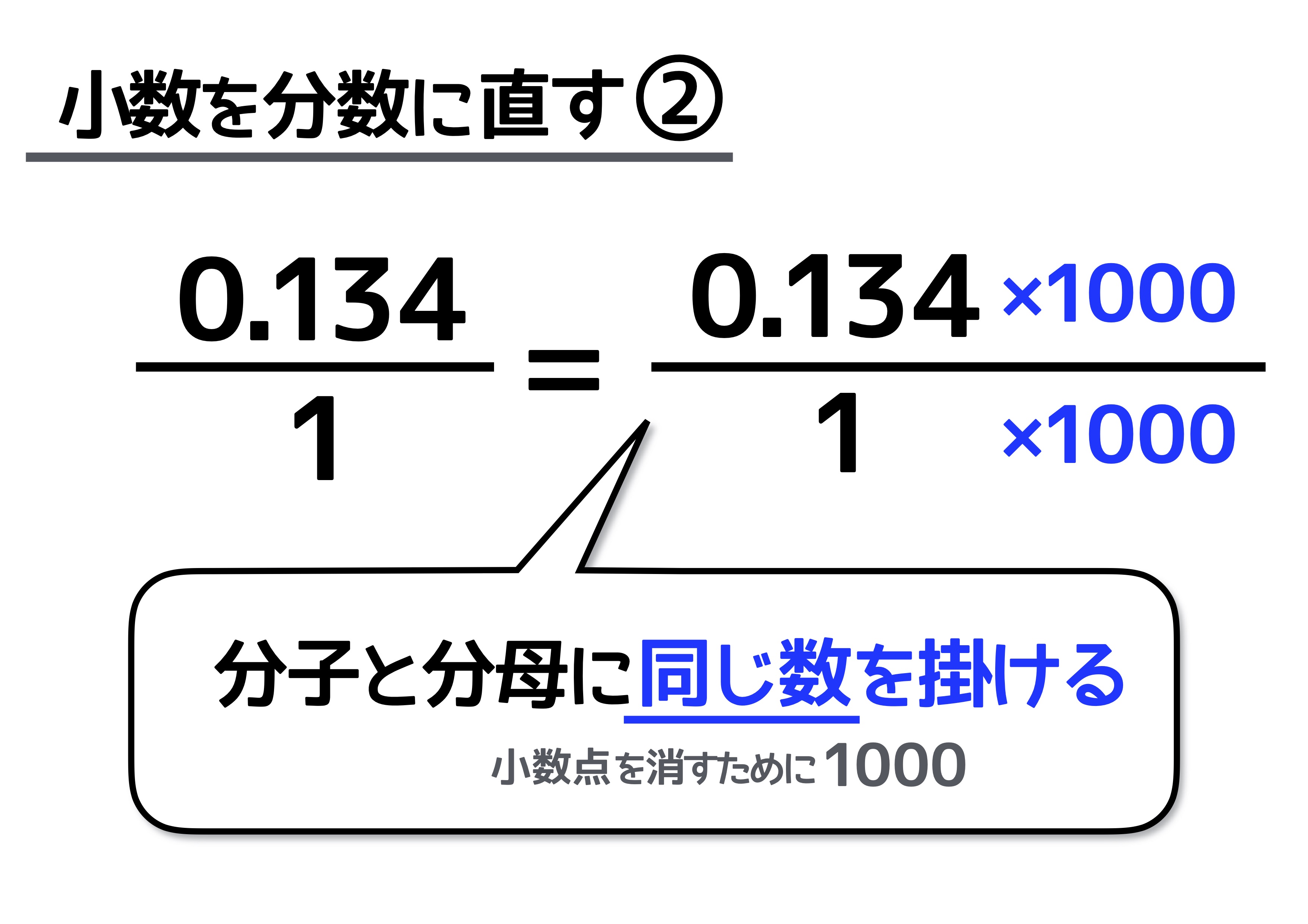
整数→3 分数→1／3 ここで分けた整数3の部分は、そのまま時間を付ければOKです。 つまり、3時間ということです。 あとは、残っている1／3を直すだけ。 解き方の手順②分数を時間に直す 1／3時間は、60分（1時間）を3等分にしたうちの1こ分という分数を小数に直すには，どうすればいいの 9 4分の3や12分の7などを，小数に直す方法を教えて 10 分数が整数になる場合があるの 11 小数を分数に直すには，どうすればいいの 12 09や012や0275を，分数に直す方法を教えて 13 27や301などを，分数に直す方法を教えて 14 整数を分数に √6を整数に直すと？ 数学がどうしても苦手で√6を数字になおすと どういう値になるのかわかりません。 計算方法などを教えてくださるとうれしいです。 ・付け足し 数学で今「不等式と領域」というのをやっていて、 問題の答えで「(x1)2乗＋(y2)2乗＞√6」と出て、 それをグラフ(図
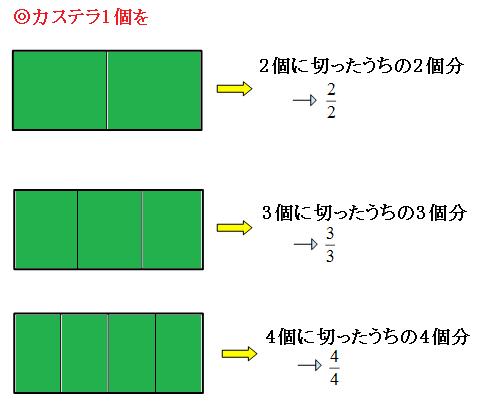
整数から分数に直す方法 整数から分数に直した例を下記に示します。 ・1 ⇒ 1/1 ・2 ⇒ 2/1 ・3 ⇒ 3/1 整数とは？1分でわかる意味、自然数、少数との違い、負の数、0、分数との関係 2を分数にすると？1分でわかる値と計算、小数と分数の関係、12、4、5、9分単位に直すには 24*60=1440を掛けます ="715"*1440 とすると 435(分)と求めることができます。 (小数誤差が問題になるようなときには分単位(整数)で計算することも有ります。) 時刻・時間の比較 topへ Excelでは時刻・時間の形式（「：」（コロン)で区切って）でセルに入力すると、自動的に分数にある2つの意味のうち、第一義 （ 1を3等分したものを2つ集めたもの＝ 2/3 ）は3年生で学習します。 このページのプリントでは、第二義 （ 2を3でわったもの＝ 2/3 ）つまり、わり算の商を表すための分数 (商の分数）を中心に、その表し方や計算方法を練習します。 （プリント10枚） 小学6
整数を分数に直すのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath | 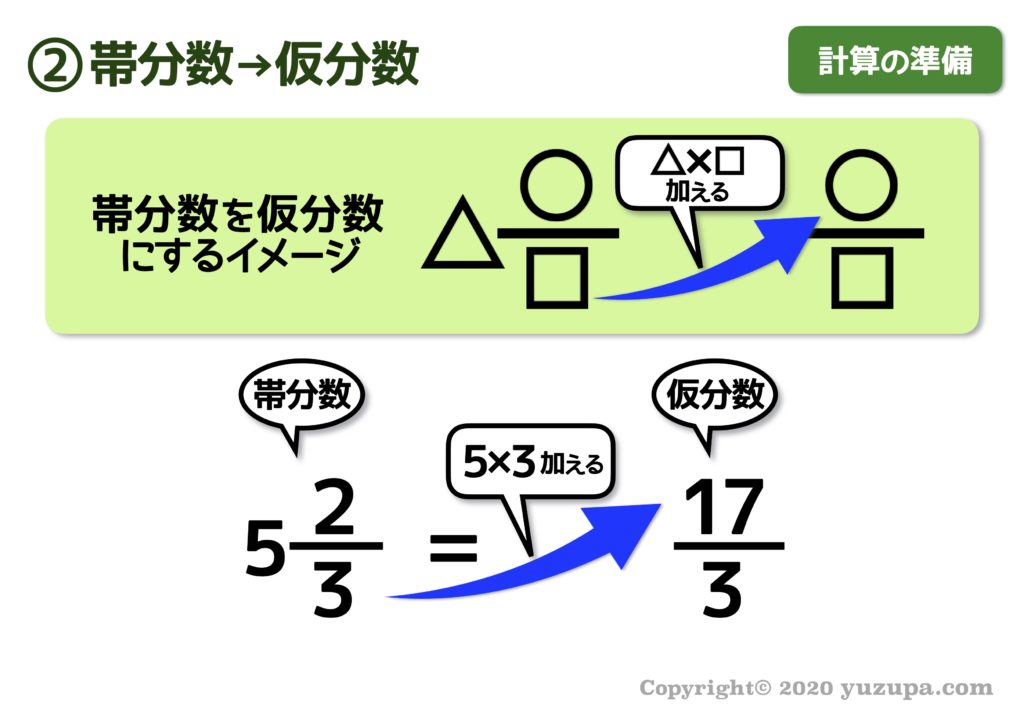 探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |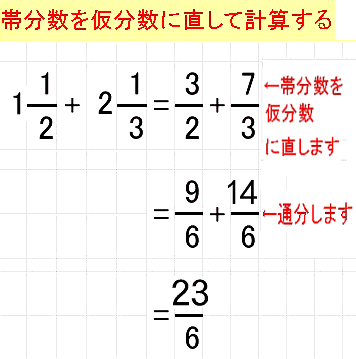
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |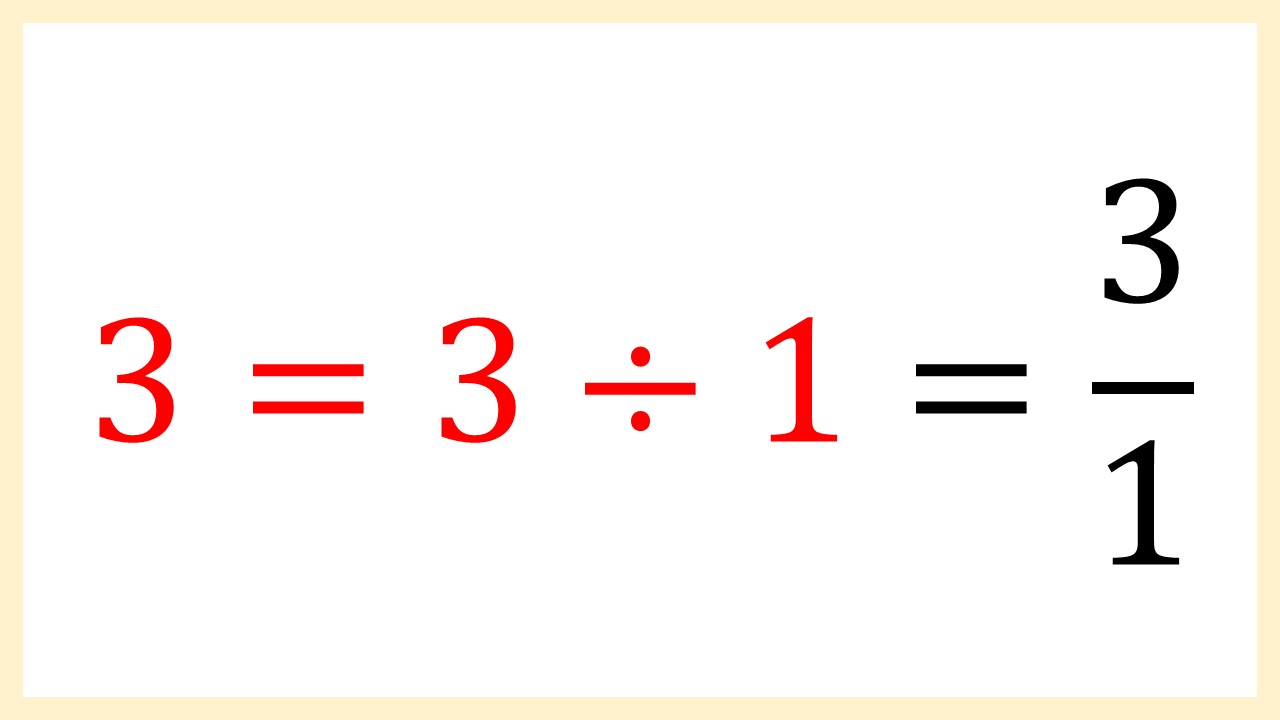
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |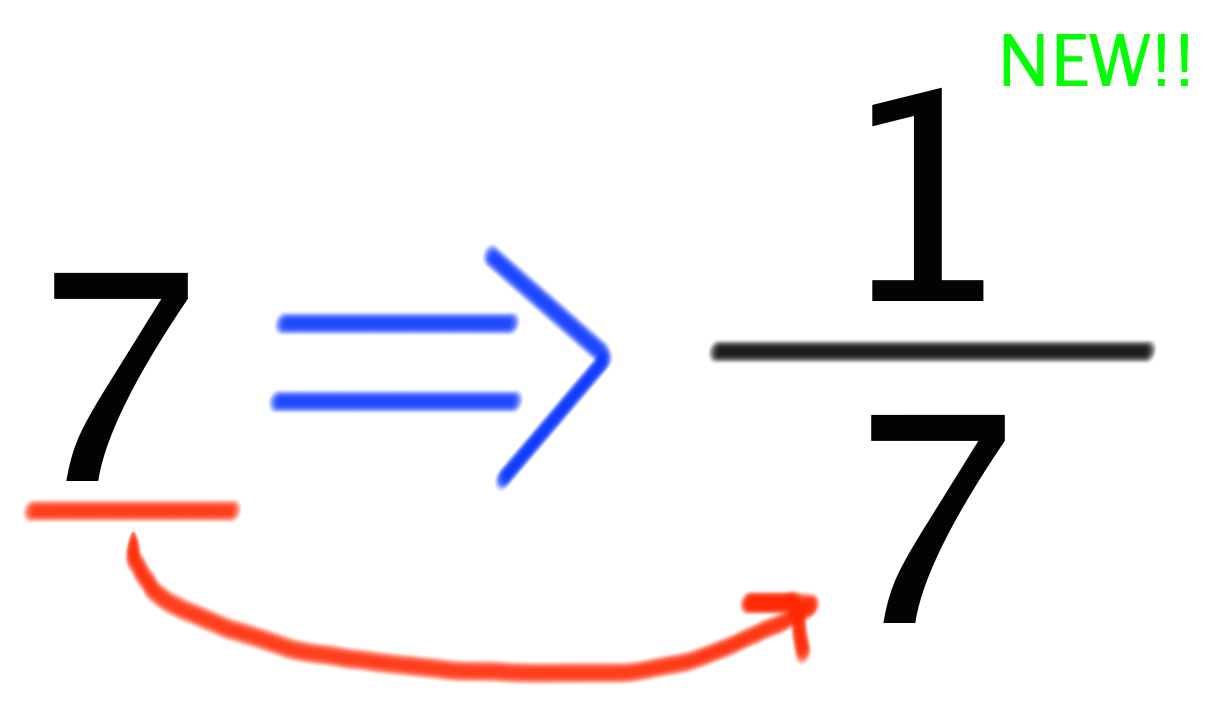
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath | 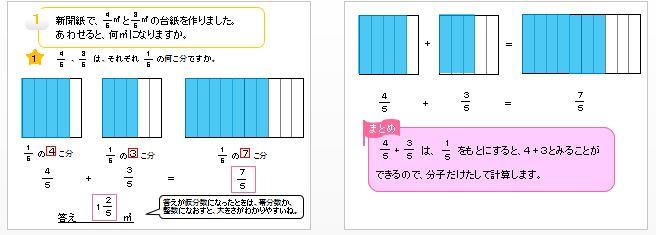 探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |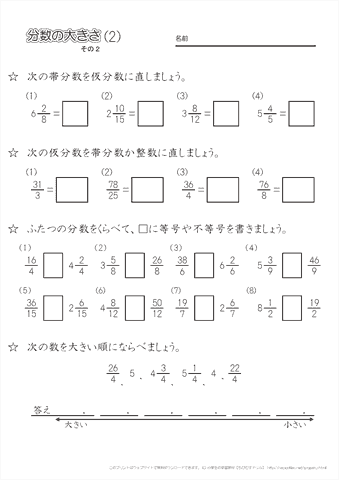
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |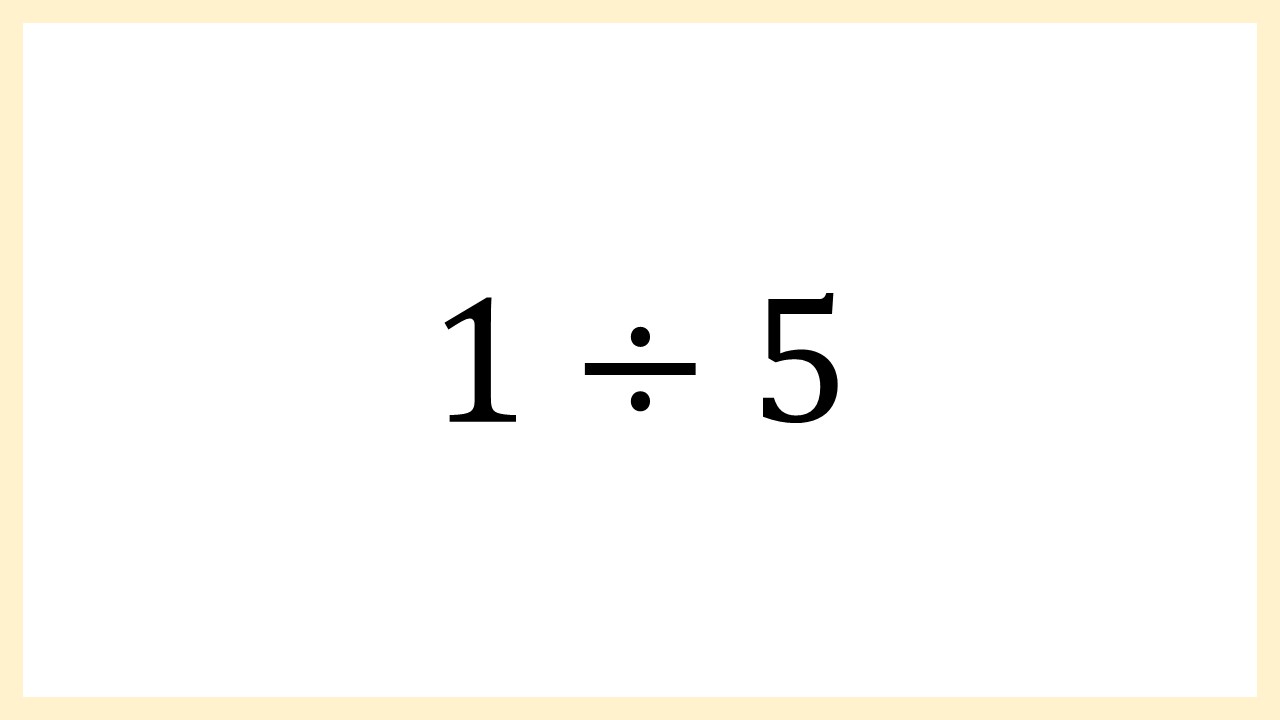
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath | 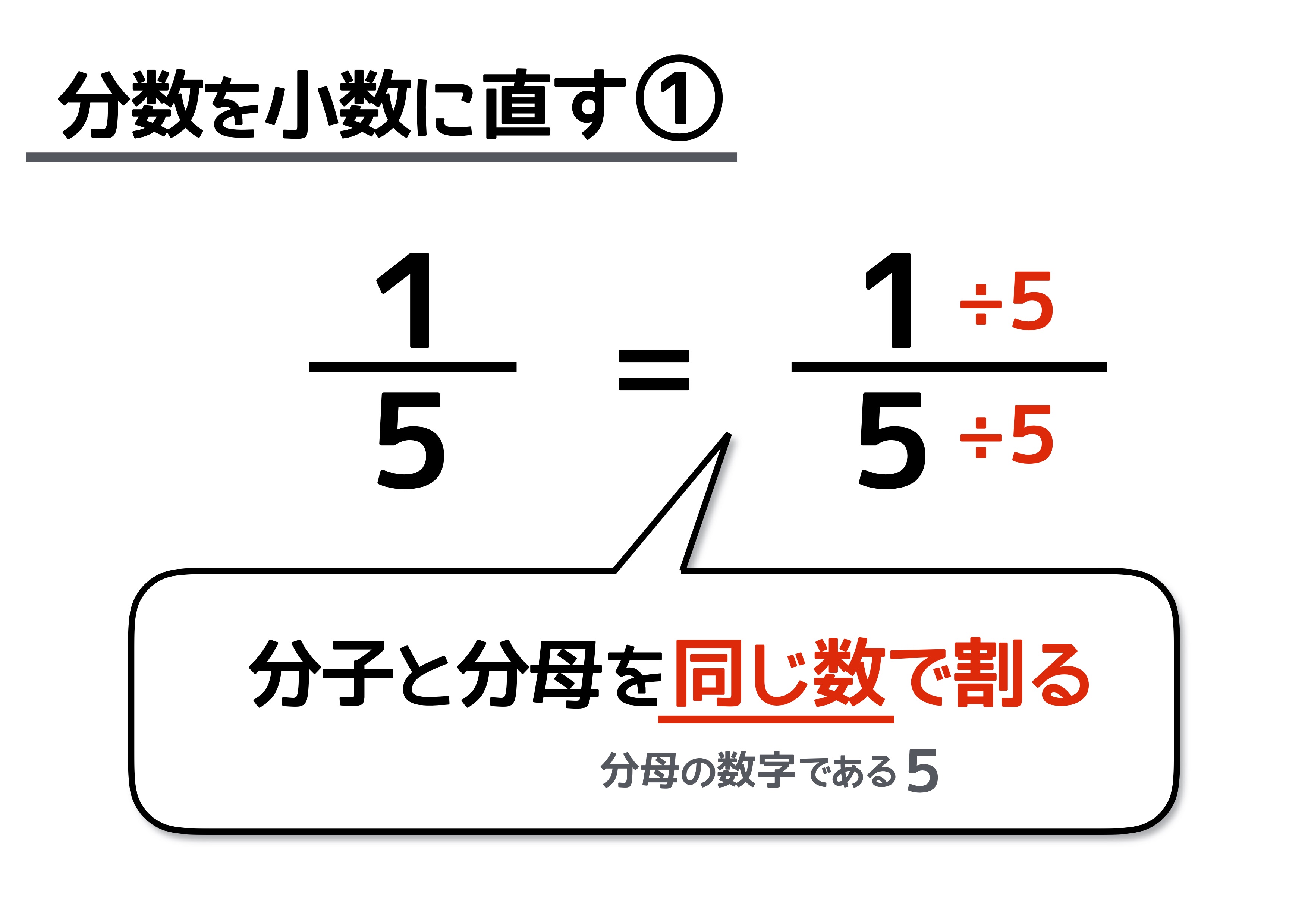 探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath | 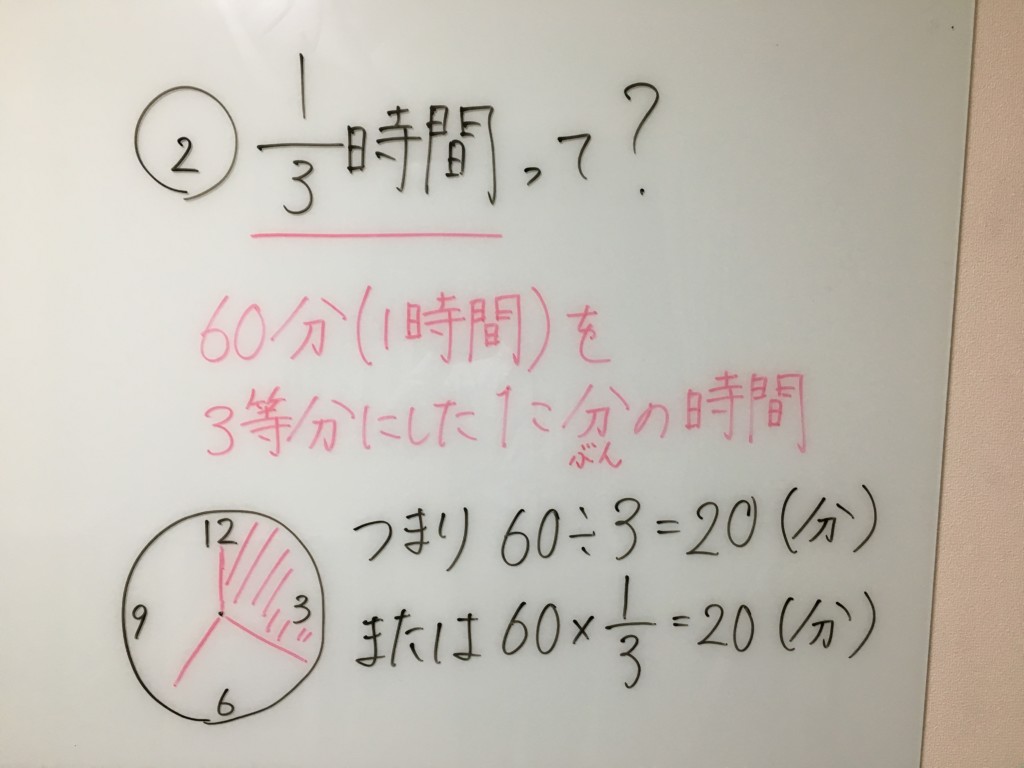 探究の自主勉 授業がんばりmath |
探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath | 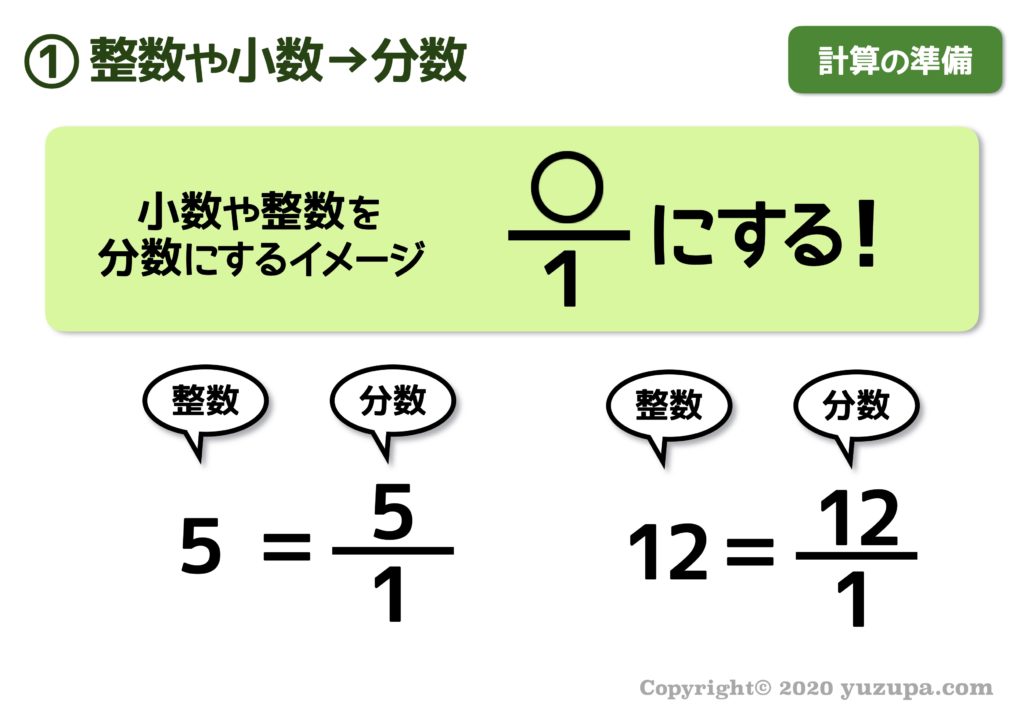 探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |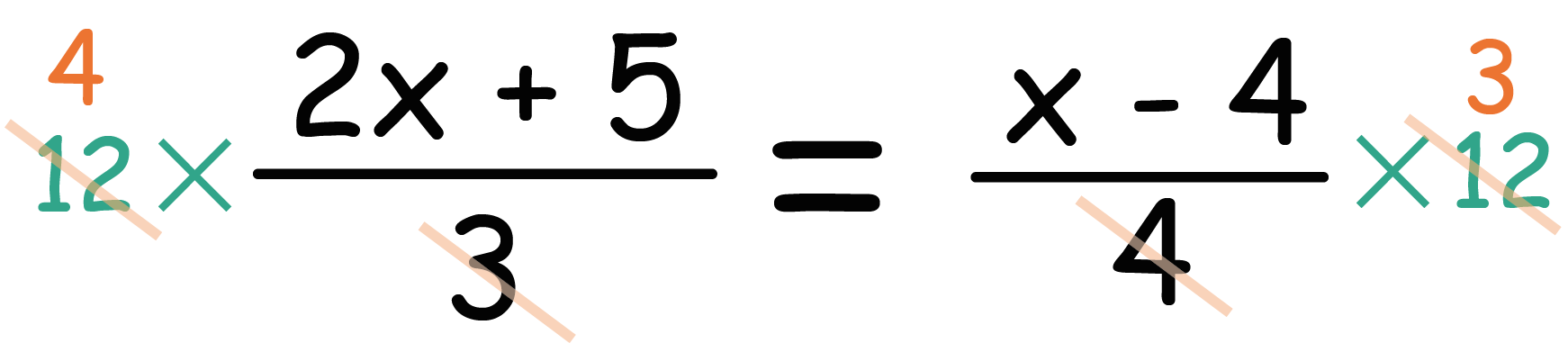
探究の自主勉 授業がんばりmath | 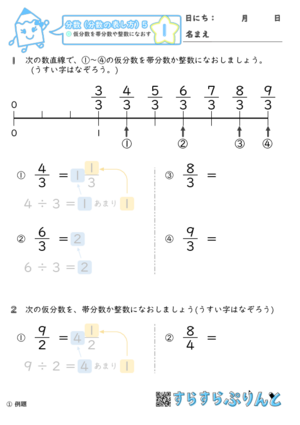 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |
探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 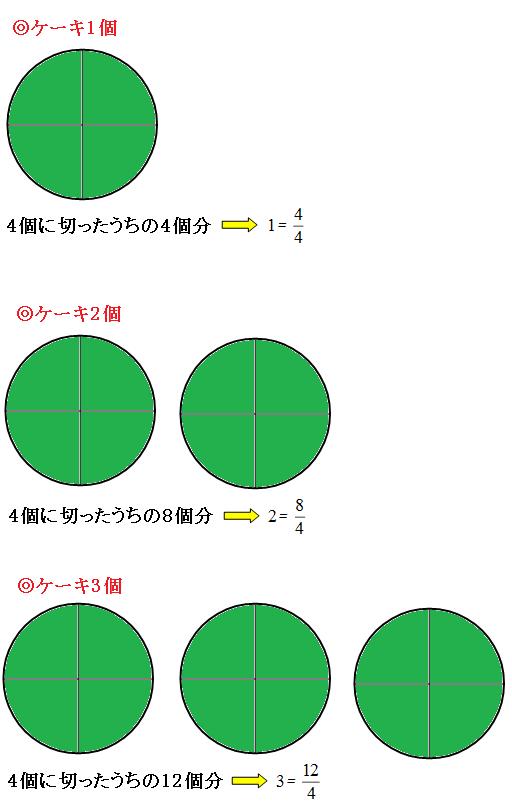 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |  探究の自主勉 授業がんばりmath |
 探究の自主勉 授業がんばりmath | 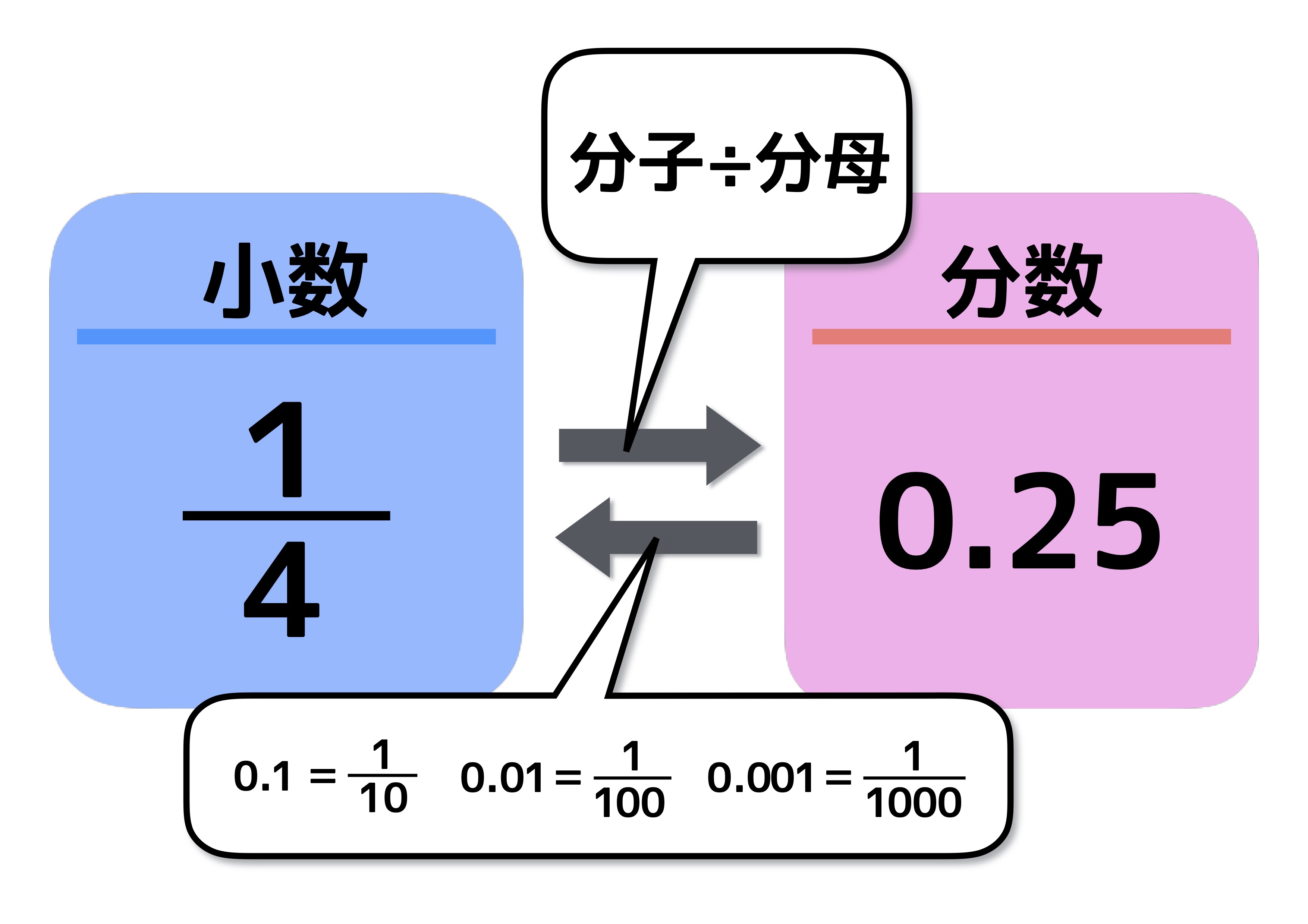 探究の自主勉 授業がんばりmath |
分数を割り算に直す確認問題集 問題編 1次の分数を、割り算に直しましょう。 （1）3/4 （2）9/2 （3）7/8 （4）11/ （5）22/31 解答編 1次の分数を、割り算に直しましょう。 （1）3/4 分子（上の段）を割り算記号の左に、分母（下の段）を割り算記号の右にもってくるので、答えは3÷4です 整数を分数に直す時、分母(下)は「1」になります。それで分子(上)は、その直したい整数の数になります。例えば、7を分数に直すと、下は1で上が7なので、「1分の7」ということになります。 ここから下は例題です。 12→1分の12 9→1分の9 17→1分の17 3→1分の3 5→1分の5 本当に分かりにくかったら
Incoming Term: 整数を分数に直す, 整数を分数に直す 計算機,
0 件のコメント:
コメントを投稿